近日，北京化工大学数理学院门曰阳团队与北京工业大学徐永利团队合作，首次提出了基于几何强混合序列（Geometrically Strongly Mixing Sequence）的DNN快速学习速率理论框架，为非独立样本下的深度学习算法提供了理论支撑。该成果发表于人工智能领域顶级期刊《IEEE Transactions on Neural Networks and Learning Systems》。

研究背景与挑战

在机器学习基础理论研究领域，深度神经网络（DNN）的收敛性分析一直是核心课题之一。现有研究大多基于样本独立性假设，然而现实场景中的数据往往具有复杂的依赖结构，例如语音识别、金融预测、时间序列分析等应用。传统理论分析通常假设样本独立，但实际数据（如时间序列、传感器网络数据）常呈现复杂依赖性。混合序列是刻画依赖关系的重要工具，然而其与深度学习的结合研究长期处于空白状态。本文的核心科学问题是：“在非独立数据条件下，DNN的收敛性结论是否依然成立？”

 核心方法与创新

本研究聚焦于DNN回归问题，假设样本序列满足几何强混合性，并对基于经验风险最小化（ERM）的DNN回归算法进行了误差分析。与独立样本情形不同，在混合序列设定下，算法的学习性能不再仅由样本数量决定，而是由“有效观测数”所主导。研究团队通过巧妙运用混合概率不等式，对样本误差进行了精确估计，并结合已有的DNN逼近误差分析，最终建立了DNN回归在几何强混合序列下的快速收敛率。该收敛率在混合序列的关键参数趋于无穷大时，可退化为独立样本情形下的收敛率，从而体现了理论结果的自然推广性。

 实验验证

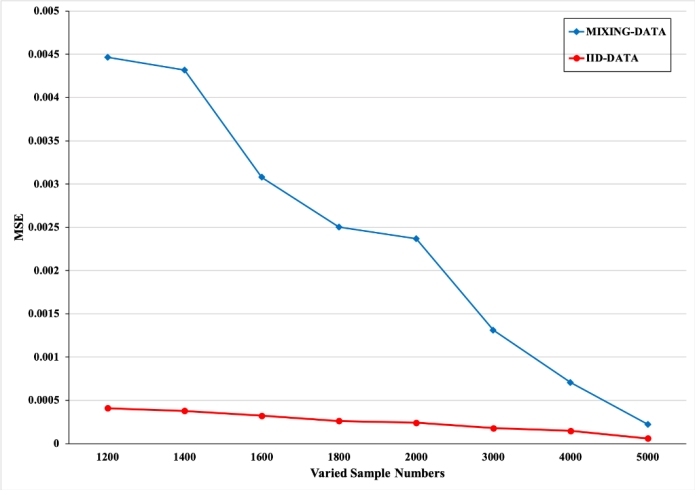
为验证理论结果，研究团队设计了一系列数值实验，通过自回归（AR）模型生成具有几何强混合性质的数据集，并采用随机梯度下降（SGD）方法近似求解ERM问题，得到预测函数。实验比较了非独立数据与独立数据下的学习表现。结果显示，在相同训练样本量下，基于AR模型生成的非独立数据所获得的误差大于独立数据情形，但随着样本量增加，两者误差差距逐渐缩小，与理论分析一致。

文章信息
Yueyang Men, Liang Li, Ziqing Hu, et al. Learning Rates of Deep Nets for Geometrically Strongly Mixing Sequence[J]. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(3): 5826-5832.
DOI: 10.1109/TNNLS.2024.3371025

 期刊简介

《IEEE Transactions on Neural Networks and Learning Systems》是人工智能领域的国际顶级期刊，聚焦神经网络与学习系统的前沿理论与方法，涵盖深度学习、强化学习等重要研究方向。